(Những độc giả không chuyên (hoặc có trực giác) có thể bỏ qua chương này vì nó đi sâu chi tiết vào mô hình đường cong hình chuông. Đồng thời, nếu không thuộc nhóm những người may mắn không biết về đường cong hình chuông, bạn cũng có thể bỏ qua.)
KHÔNG ĐÁNG MỘT LY RƯỢU PASTIS ■ SAI SÓT CỦA QUÉTELET ■ MỘT NGƯỜI BÌNH THƯỜNG LÀ MỘT CON QUỶ ■ HÃY TÔN SÙNG NÓ ■ CÓ HAY KHÔNG MỘT THỬ NGHIỆM KHÔNG QUÁ VĂN CHƯƠNG
Hãy quên hết tất cả những gì bạn nghe được ở trường đại học về thống kê hoặc lý thuyết xác suất. Thậm chí càng tốt nếu bạn chưa từng tham dự lớp học nào như thế. Hãy bắt đầu lại từ đầu.
Tôi đang chuẩn bị quá cảnh ở sân bay Frankfurt trên đường từ Oslo đến Zurich vào tháng 12 năm 2001.
Tôi có nhiều thời gian ở sân bay và đây là một cơ hội tuyệt vời để mua một thỏi sôcôla đen châu Âu, đặc biệt khi thuyết phục được bản thân mình rằng hàm lượng calories ở sân bay chẳng có ý nghĩa gì. Trong số những tờ giấy bạc mà người bán hàng trả lại cho tôi có một tờ 10 mác Đức – bạn có thể nhìn thấy hình quét (phi pháp) của tờ tiền này ở trang bên. Vào thời điểm đó, chỉ còn vài ngày nữa là những tờ mác Đức đó sẽ phải ngừng lưu thông vì châu Âu sắp chuyển sang sử dụng đồng Euro. Tôi đã giữ nó làm kỷ niệm. Trước khi sử dụng đồng Euro, châu Âu có rất nhiều đơn vị tiền tệ – điều có lợi cho các máy in tiền, những người đổi tiền và dĩ nhiên cả những người giao dịch tiền tệ (ít nhiều) giống như tác giả hèn mọn đang viết cuốn sách này. Khi nhắm nháp thỏi sôcôla đen châu Âu và nuối tiếc nhìn tờ giấy bạc đó, tôi gần như lặng người. Lần đầu tiên, đột nhiên tôi nhận thấy có điều gì kỳ lạ trong đó. Tờ giấy bạc có hình chân dung của Carl Friedrich Gauss và đường cong hình chuông mang tên ông.

Tờ giấy bạc 10 đồng mác Đức cuối cùng với hình Gauss và bên phải ông là đường cong hình chuông của Mediocristan.
Điều đáng mỉa mai ở đây là vật thể cuối cùng có liên quan đến đơn vị tiền tệ của Đức lại chính là một đường cong: đồng reichsmark (theo cách gọi trước đây) đã tăng từ bốn tờ một đô-la lên đến bốn nghìn tỷ tờ một đô-la chỉ trong khoảng vài năm trong thập niên 20, một kết quả giúp bạn hiểu rằng đường cong hình chuông không mô tả được tính ngẫu nhiên trong các biến động của tiền tệ. Tất cả những gì bạn cần để chối bỏ đường cong hình chuông này là để cho một biến động xảy ra một lần, và chỉ một lần duy nhất – khi đó hãy xem xét kết quả của nó. Thế nhưng, đã có đường cong hình chuông và bên cạnh nó là Giáo sư Tiến sĩ Gauss, một người không hấp dẫn và hơi lạnh lùng, và dĩ nhiên không phải là người mà tôi muốn dành thời gian cùng đi dạo ngoài ban công, uống pastis và tán gẫu. Thật tồi tệ là đường cong hình chuông này được các nhà điều phối và các chủ ngân hàng trung ương – những người mặc complê đen và có lối nói chuyện nhàm chán về các đơn vị tiền tệ – sử dụng như một công cụ đo lường rủi ro.
Như tôi đã nói, quan điểm chính của Gauss là hầu hết các quan sát đều xoay quanh mediocre, mức bình thường; khả năng xảy ra một độ lệch ngày càng suy yếu nhanh hơn (theo hàm mũ) khi bạn càng rời xa mức bình thường này. Nếu bạn chỉ có duy nhất một mẩu tin thì đó sẽ là: Sự gia tăng đầy kịch tính trong tốc độ suy yếu của các khả năng khi bạn rời xa trung tâm, hay rời xa mức bình thường. Hãy xem danh sách bên dưới để hiểu rõ hơn về điều này. Tôi sẽ lấy ví dụ về một định lượng Gauss, như chiều cao chẳng hạn, và đơn giản hóa nó một chút để bạn dễ hiểu hơn. Giả định rằng chiều cao trung bình (nam, nữ) là 1,67m hay 5 feet 7 inch. Giả sử những gì tôi gọi là đơn vị tính độ lệch (unit of devitation) ở đây bằng 10cm. Hãy nhìn vào số gia trên mức 1,67m và xem xét xác xuất của những người có chiều cao như thế. 67
Cao hơn trung bình 10cm (tức cao hơn 1,77m, hoặc 5,10 feet): tỷ lệ là 1 trên 6,3
Cao hơn trung bình 20cm (tức cao hơn 1,87m, hoặc 6,2 feet): 1 trên 44
Cao hơn trung bình 30cm (tức cao hơn 1,97m, hoặc 6,6 feet): 1 trên 740
Cao hơn trung bình 40cm (tức cao hơn 2,07m, hoặc 6,9 feet): 1 trên 32.000
Cao hơn trung bình 50cm (tức cao hơn 2,17m, hoặc 7,1 feet): 1 trên 3.500.000
Cao hơn trung bình 60cm (tức cao hơn 2,27m, hoặc 7,5 feet): 1 trên 1.000.000.000
Cao hơn trung bình 70cm (tức cao hơn 2,3 7m, hoặc 7,9 feet): 1 trên 780.000.000.000
Cao hơn trung bình 80cm (tức cao hơn 2,47m, hoặc 8,1 feet): 1 trên 1.600.000.000.000.000
Cao hơn trung bình 90cm (tức cao hơn 2,57m, hoặc 8,5 feet): 1 trên 8.900.000.000.000.000.000
Cao hơn trung bình 100cm (tức cao hơn 2,67m, hoặc 8,9 feet): 1 trên 130.000.000.000.000.000.000.000 …và,
Cao hơn mức trung bình 110cm (tức là cao hơn 2,11m hoặc 9,1 feet): tỷ lệ là 1 trên
36,000,000,000,000,000,000,000,000,000,000,000,000,000,000,00
0,000,000,000,000,000,000,000,000,000,000,000,000,000,000.
Lưu ý rằng ngay sau đó, với 22 độ lệch, hoặc cao hơn trung bình 220cm, tỷ lệ đó sẽ đạt đến googol, tức là 1 với 100 con số 0 sau đó.
Mục đích của danh sách này là để minh họa cho gia tốc. Hãy nhìn vào sự chênh lệch về xác suất giữa mức cao hơn trung bình 60 và 70cm: chỉ với mức tăng thêm 4 inch, tỷ lệ đã thay đổi từ 1 trên 1 tỷ người thành 1 trên 780 tỷ người! Còn đối với mức nhảy vọt giữa 70 và 80cm: chỉ thêm 4 inch trên mức trung bình, tỷ lệ này đã thay đổi từ 1 trên 780 tỷ người thành 1 trên 1,6 triệu tỷ! 68
Sự suy giảm mạnh mẽ về khả năng tình cờ gặp phải một điều gì đó chính là thứ cho phép bạn lờ đi các yếu tố ngoại lai. Chỉ có một đường cong mới có thể tạo ra sự sụt giảm này, và đó chính là đường cong hình chuông (và những biến thể phi thang bậc của nó)
Để so sánh, hãy nhìn vào khả năng trở nên giàu có ở châu Âu. Giả sử rằng sự giàu có ở đó có tính thang bậc, tức là thuộc tập hợp Mandelbrot. (Đây không phải là một mô tả chính xác về sự giàu có ở châu Âu; nó đã được đơn giản hóa để nhấn mạnh đến tính lôgic của sự phân bổ theo thang bậc.) 69
Sự phân bổ tài sản theo thang bậc
Những người có thu nhập trên 1 triệu euro: tỷ lệ là 1 trên 62,5
Cao hơn 2 triệu euro: 1 trên 250
Cao hơn 4 triệu euro: 1 trên 1.000
Cao hơn 8 triệu euro: 1 trên 4.000
Cao hơn 16 triệu euro: 1 trên 16.000
Cao hơn 32 triệu euro: 1 trên 64.000
Cao hơn 320 triệu euro: 1 trên 6.400.000
Tốc độ suy giảm ở đây vẫn không đổi (hoặc không suy giảm)! Khi bạn nhân đôi số tiền lên, số người đạt được mức đó giảm xuống còn 1/4, bất kể ở mức nào, dù là 8 triệu euro hay 16 triệu euro. Tóm lại, ví dụ này minh họa cho sự khác biệt giữa Mediocristan và Extremistan.
Hãy nhớ lại phần so sánh giữa yếu tố thang bậc và phi thang bậc ở Chương 3. Tính thang bậc có nghĩa là không có một yếu tố nào có thể làm cho bạn chậm lại. Dĩ nhiên, mức Extremistan thuộc tập hợp Mandelbrot có thể diễn ra dưới nhiều hình thức. Hãy xem ví dụ về sự giàu có trong một bối cảnh hết sức tập trung của Extremistan; ở đó, nếu bạn nhân đôi tài sản, số người đạt được mức tài sản đó sẽ giảm đi một nửa. Về mặt định lượng, kết quả này khác với ví dụ trên, nhưng nó tuân theo cùng một lôgic.
Những người có tài sản trên 1 triệu euro: 1 trên 63
Cao hơn 2 triệu euro: 1 trên 125
Cao hơn 4 triệu euro: 1 trên 250
Cao hơn 8 triệu euro: 1 trên 500
Cao hơn 16 triệu euro: 1 trên 1.000
Cao hơn 32 triệu euro: 1 trên 2.000
Cao hơn 320 triệu euro: 1 trên 20.000
Cao hơn 640 triệu euro: 1 trên 40.000
Nếu tài sản thuộc dạng Gauss, chúng ta sẽ quan sát độ lệch so với mức 1 triệu euro.
Sự phân bổ tài sản theo quy luật Gauss
Những người có thu nhập cao hơn 1 triệu euro: 1 trên 63
Cao hơn 2 triệu euro: 1 trên 127.000
Cao hơn 3 triệu euro: 1 trên 14.000.000.000
Cao hơn 4 triệu euro: 1 trên 886.000.000.000.000.000
Cao hơn 8 triệu euro:
1 trên 16.000.000.000.000.000.000.000.000.000.000.000
Cao hơn 8 triệu euro: 1 trên… không cái máy tính nào của tôi có thể thực hiện phép tính này
Điều tôi muốn chỉ ra với những danh sách trên là sự khác nhau về định tính trong hệ biến hóa này. Như tôi đã nói, hệ biến hóa thứ hai có tính thang bậc; nó không “ngược gió”. Lưu ý rằng một thuật ngữ khác về tính thang bậc này là định luật lũy thừa.
Nếu chỉ biết rằng chúng ta đang sống trong một môi trường định luật lũy thừa cũng không nói lên được gì nhiều. Vì sao? Vì chúng ta phải đánh giá các hệ số trong cuộc sống thực, điều này khó hơn nhiều so với một khuôn khổ Gauss. Chỉ có đường cong Gauss mới tạo ra các thuộc tính của nó khá nhanh chóng. Phương pháp mà tôi đề xuất là một cách tổng quát để nhìn nhận thế giới thay cho một giải pháp cụ thể.
Hãy nhớ điều nay: Các biến số đường cong hình chuông Gauss sẽ đi “ngược gió” – điều khiến cho các xác suất giảm xuống với tốc độ ngày càng nhanh khi bạn càng cách xa mức bình thường, trong khi “các yếu tố thang bậc”, hay các biến số Mandelbrot, lại không gặp phải giới hạn như thế. Đó chính là phần lớn những gì bạn cần biết 70
Hãy cùng xem xét kỹ hơn bản chất của sự bất bình đẳng này. Trong khuôn khổ Gauss, sự bất bình đẳng sẽ giảm xuống khi độ lệch ngày càng lớn – gây ra bởi sự gia tăng của tốc độ suy giảm. Điều này không xảy ra với tính thang bậc sự bất bình đẳng luôn duy trì xuyên suốt từ đầu đến cuối. Sự bất bình đẳng giữa những người cực giàu ở đây cũng giống với sự bất bình đẳng giữa những người giàu – nó không giảm đi chút nào. 71
Hãy xem xét hiệu ứng này. Hãy chọn ra hai người Mỹ ngẫu nhiên cùng kiếm được 1 triệu đô-la mỗi năm. Mức phân chia khả dĩ nhất cho thu nhập tương ứng của mỗi người là bao nhiêu? Ở Mediocristan, tổ hợp có thể xảy ra nhất là mỗi người nửa triệu. Ở Extremistan, con số sẽ là 50.000 đô-la và 950.000 đô-la.
Tình huống này thậm chí còn lệch hơn nữa đối với doanh số bán sách. Nếu tôi nói với bạn rằng hai tác giả bán được tổng cộng 1 triệu cuốn sách, tổ hợp có thể xảy ra nhất là một người bán được 993.000 cuốn còn người kia được 7.000 cuốn. Điều này rất dễ xảy ra so với trường hợp mỗi người bán được 500.000 cuốn. Đối với bất kỳ số tượng lớn nào, mức phân chia đó sẽ càng bất cân xứng. Vì sao lại như thế? Bài toán về chiều cao cho chúng ta một sự so sánh. Nếu tôi nói với bạn rằng tổng chiều cao của hai người là 14 feet, bạn sẽ nhận thấy rằng mức phân chia khả dĩ nhất là mỗi người cao 7 feet, chứ không phải người này cao 2 feet và người kia cao 12 feet; cũng không thể người này 8 feet còn người kia 6 feet! Số người có chiều cao trên 8 feet hiếm đến mức một tổ hợp như thế sẽ không thể xảy ra.
Bạn có bao giờ nghe về quy luật 80/20 chưa? Đó là một dạng phổ biến của định luật lũy thừa – thật ra, đó chính là cách mọi thứ bắt đầu khi Vilfredo Pareto quan sát thấy rằng 80% đất đai ở Ý là thuộc quyền sở hữu của 20% dân số nước này. Một số người sử dụng quy luật này để ám chỉ rằng 80% công việc được thực hiện bởi 20% dân số. Hoặc 80% nỗ lực góp phần tạo ra 20% thành quả và ngược lại.
Xét về mặt chân lý thì cách diễn giải này không khiến bạn ấn tượng: chúng ta có thể dễ dàng gọi nó là quy luật 50/01, tức là 50% công việc xuất phát từ 1% số công nhân. Lối trình bày này càng khiến cho thế giới có vẻ bất công hơn, tuy nhiên hai công thức này chính là một. Bằng cách nào? Nếu có sự bất bình đẳng thì khi đó, những yếu tố cấu thành 20% trong quy luật 80/20 đó cũng đồng thời có sự đóng góp không đồng đều – chỉ một vài trong số đó tạo ra phần lớn kết quả. Có thể giới hạn con số này xuống còn khoảng 1 trên 100 góp phần tạo ra hơn nửa trong toàn kết quả.
Quy luật 80/20 này không chỉ mang tính ẩn dụ, nó không phải là một quy luật, càng không phải là một định luật cứng nhắc. Trong lĩnh vực kinh doanh sách ở Mỹ, tỷ lệ đó có thể là 97/20 (tức là 97% doanh số bán sách được tạo ra bởi 20% tác giả); sẽ càng tồi tệ hơn nếu bạn tập trung vào lĩnh vực sách phi tiểu thuyết (20 trong số gần 8000 cuốn sách đại diện cho một nửa doanh thu).
Ở đây xin lưu ý rằng không phải tất cả đều có tính bất định. Trong một số tình huống, bạn có thể có sự tập trung của quy luật 80/20 với các thuộc tính rất có thể dự đoán và theo dõi được – điều cho phép đưa ra quyết định rõ ràng vì bạn có thể xác định trước vị trí của mức 20% đầy ý nghĩa đó. Những tình huống này rất dễ kiểm soát. Ví dụ, Malcolm Gladwell đã viết trong một bài báo trên tờ The New Yorker rằng phần lớn các hành động lạm dụng/ngược đãi tù nhân đều do một số lượng nhỏ những tên cai ngục tàn ác gây ra. Hãy thanh lọc những tên cai ngục này và khi đó tỷ lệ lạm dụng tù nhân sẽ giảm một cách đáng kể. (Ngược lại, trong lĩnh vực xuất bản, bạn không biết trước được cuốn sách nào sẽ giành chiến thắng.
Đối với các cuộc chiến cũng vậy, vì bạn không biết trước được xung đột nào sẽ giết chết một phần cư dân của hành tinh này).
Ở đây tôi xin tóm tắt và nhắc lại các luận cứ đã được trình bày xuyên suốt cuốn sách này. Các phép đo về tính bất định được dựa trên đường cong hình chuông rõ ràng không chú ý đến xác suất, tác động của những bước nhảy mạnh hoặc của những điểm gián đoạn, và do đó không thể áp dụng trong Extremistan. Việc sử dụng chúng cũng giống như tập trung vào đám cỏ và bỏ qua những cái cây (to). Mặc dù hiếm xảy ra trường hợp không thể dự đoán được những độ lệch lớn, nhưng chúng ta không thể gạt bỏ chúng như những yếu tố ngoại lai, bởi chúng có tác động tích lũy rất lớn.
Phương pháp nhìn nhận thế giới theo kiểu truyền thống của Gauss bắt đầu bằng việc tập trung vào những thứ bình thường, sau đó mới đến các trường hợp ngoại lệ hoặc những cái gọi là yếu tố ngoại lai. Nhưng còn có một cách nữa, đó là bắt đầu xem xét các trường hợp ngoại lệ rồi sau đó mới đến những thứ bình thường với tư cách là yếu tố phụ thuộc.
Tôi đã nhấn mạnh rằng có hai biến thể của tính ngẫu nhiên, khác nhau về chất, như nước và không khí. Một cái không quan tâm đến các biến cố cực độ, còn một cái lại chịu tác động rất lớn bởi các biến cố cực độ. Một cái không tạo ra Thiên Nga Đen, còn một cái thì có. Chúng ta không thể thảo thuận về chất khí (gas) giống như cách thảo luận về chất lỏng (liquid). Và nếu có thể làm được điều đó, chúng ta cũng sẽ không gọi biện pháp đó là “phép tính xấp xỉ”. Một chất khí không thể nào “xấp xỉ” một chất lỏng.
Chúng ta có thể tận dụng cách tiếp cận của Gauss trong các biến số, mà theo đó có một lý do hợp lý để phần lớn nhất không quá cách xa mức trung bình. Nếu có trọng lực hút các con số lại với nhau, hoặc nếu có các giới hạn tự nhiên ngăn cản các quan sát cực lớn, chúng ta sẽ kết thúc ở Mediocristan. Nếu có các lực cân bằng mạnh mẽ có thể đưa mọi thứ nhanh chóng trở lại sau khi bị lệch ra khỏi trạng thái cân bằng, thì một lần nữa, bạn lại có thể sử dụng phương pháp Gauss. Nếu không thì hãy quên nó đi. Đây là lý do vì sao phần lớn kinh tế học đều dựa trên khái niệm về tính cân bằng: ngoài những lợi ích khác, nó còn cho phép bạn giải quyết các hiện tượng kinh tế như một yếu tố mang thuộc tính Gauss.
Xin lưu ý, ở đây tôi không có ý nói rằng kiểu ngẫu nhiên Mediocristan không cho phép xảy ra một số hiện tượng cực độ nào đó. Nhưng ở đây tôi muốn nói là nó hiếm đến mức chúng không có vai trò quan trọng trong tổng thể. Hiệu ứng của những hiện tượng cực độ đó nhỏ đến mức thảm hại và càng suy giảm khi dân số ngày càng tăng.
Ở đây hơi đi sâu vào chuyên môn một chút, nếu bạn có một bảng phân loại những người khổng lồ và những người tí hon, tức là các quan sát cách nhau vài cấp cường độ, bạn có thể vẫn thuộc Mediocristan. Bằng cách nào? Giả sử bạn có một ví dụ mẫu gồm 1000 người, với một chuỗi rộng lớn dao động từ người tí hon đến người khổng lồ. Bạn có thể nhìn thấy nhiều người khổng lồ trong ví dụ của mình, chứ không phải một trường hợp hiếm hoi. Chiều cao trung bình sẽ không bị tác động bởi sự xuất hiện của người khổng lồ đó, bởi một vài trong số những người khổng lồ này sẽ trở thành một phần trong ví dụ của bạn, và chiều cao trung bình trong ví dụ của bạn có thể ở mức cao. Nói cách khác, quan sát lớn nhất không thể quá cách xa so với mức trung bình. Mức trung bình phải luôn bao gồm hai loại, những người khổng lồ và những người tí hon, sao cho cả hai không trở nên hiểm hoi – trừ khi bạn có một người cực kỳ khổng lồ và một người cực kỳ tí hon trong những trường hợp rất hiếm. Đây sẽ là Mediocristan với độ lệch lớn.
Xin lưu ý một lần nữa về nguyên tắc sau: biến cố càng hiếm thì sai số trong dự đoán xác suất xảy ra của nó càng cao – ngay cả khi sử dụng đường cong Gauss.
Tôi sẽ cho bạn thấy cách thức mà đường cong hình chuông Gauss làm mất đi tính ngẫu nhiên của cuộc sống – đây là lý do khiến nó trở nên phổ biến. Chúng ta thích nó vì nó tạo ra sự ổn định! Bằng cách nào? Thông qua phép tính bình quân mà tôi sẽ thảo luận tiếp sau đây.
Hãy nhớ lại phần thảo luận về Mediocristan ở Chương 3 rằng không có quan sát đơn lẻ nào tác động đến tổng thể của bạn. Thuộc tính này sẽ ngày càng trở nên quan trọng khi dân số ngày càng tăng. Các mức trung bình sẽ ngày càng ổn định đến mức mọi mẫu thử đều trông giống nhau. Trong cuộc đời mình, tôi đã uống rất nhiều cà phê (nó là món nghiện chính của tôi). Chưa khi nào tôi để cho một tách cà phê rơi khỏi bàn giấy hay làm đổ cà phê trên bản thảo cuốn sách này (ngay cả khi ở Nga). Quả thực, cần phải nghiện cà phê dạng nhẹ thì mới có thể chúng kiến được một sự kiện như thế; nó đòi hỏi nhiều thời gian trong đời hơn mức ta tưởng tượng – khả năng xảy ra của nó quá nhỏ có tỷ lệ 1 trên quá nhiều số 0 đến mức tôi không thể viết ra hết được những số 0 đó trong thời gian rảnh rỗi của mình.
Tuy nhiên, thực tại vật lý (physical reality) có thể sẽ khiến cho tách cà phê của tôi rơi xuống – không chắc lắm nhưng có thể xảy ra. Các phần tử luôn chuyển động. Bản thân tách cà phê cũng được làm từ các phần tử chuyển động đó, vậy thì làm sao nó lại không chuyển động được chứ? Lý do đơn giản là việc để chiếc tách đó rơi khỏi bàn đòi hỏi tất cả các phần tử phải chuyển động theo cùng một hướng, và phải diễn ra liên tiếp nhiều lần như thế theo một hàng (kèm theo đó là sự chuyển động bù của chiếc bàn theo hướng ngược lại). Tất cả vài nghìn tỷ phần tử trong tách cà phê của tôi sẽ không chuyển động theo cùng một hướng; điều này sẽ không xảy ra trên đời này. Vì thế, tôi có thể yên tâm đặt tách cà phê của mình cạnh mép bàn và tập trung vào những nguồn bất ổn đáng lo ngại hơn.
Sự an toàn của tách cà phê sẽ minh họa cho khả năng chế ngự mà tính ngẫu nhiên của đường cong Gauss có thể đạt được bằng phương pháp lấy bình quân. Nếu chiếc tách của tôi là một phần tử lớn, hoặc hành động như một phần tử lớn, thì khi đó việc nó chuyển động sẽ trở thành vấn đề. Nhưng chiếc tách của tôi là sự tổng hợp của hàng nghìn tỷ các phần tử rất nhỏ.
Minh họa 7: Cách thức hoạt động của số lớn
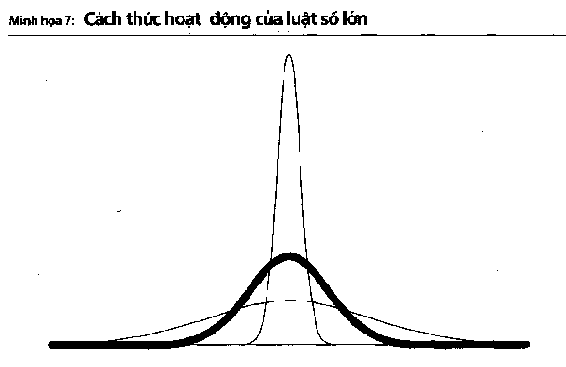
Trong Mediocristan, khi kích cỡ mẫu thử của bạn tăng lên, mức trung bình được quan sát sẽ tự hiển thị mức độ phân tán ít hơn – như bạn có thể thấy, phạm vi phân bổ này sẽ ngày càng hẹp đi. Tóm lại, đây là cách thức hoạt động (hoặc được cho là sẽ hoạt động) của mọi thứ trong lý thuyết thống kê. Sự bất định trong Mediocristan biến mất dưới phương pháp tính bình quân. Điều này minh họa cho “luật số lớn” nhàm chán này.
Các nhà quản lý sòng bạc hiểu điều này rất rõ, đó là lý do họ (nếu làm đúng cách) không bao giờ mất tiền. Chỉ đơn giản là họ không cho phép một tay cờ bạc nào đánh cược một số tiền lớn, thay vào đó, họ thích có nhiều người chơi với hàng loạt các khoản tiền đánh cược trong một giới hạn nhất định. Người chơi có thể cược tổng cộng 20 triệu đô-la, nhưng bạn không cần phải lo lắng cho sòng bạc ví dụ những lần cá cược đó diễn ra trung bình 20 đô-la/lần; sòng bạc sẽ giới hạn những khoản tiền cược ở mức tối đa nhằm đảm bảo độ an toàn cho các chủ sòng bạc. Vì thế, lợi nhuận của sòng bạc sẽ có sự thay đổi rất nhỏ cho dù hoạt động cá cược diễn ra lớn đến mức nào. Bạn sẽ không bao giờ nhìn thấy ai bước ra khỏi sòng bạc với số tiền thắng cược 1 tỷ đô-la – ít ra là trong cuộc đời này.
Ví dụ trên là một ứng dụng luật tối cao của Mediocristan: khi bạn có nhiều người chơi thì sẽ chẳng có người chơi nào có thể tác động đáng kể đến tổng thể của bạn.
Hệ quả của hình thức này là các biến đổi quanh mức trung bình của Gauss, hay còn gọi là “các sai số”, thật sự không đáng lo ngại. Chúng không đáng kể và sẽ biến mất. Chúng là những biến động đã được thuần hóa quanh giá trị trung bình.
Nếu thời đi học bạn đã từng tham dự một khóa học về thống kê (chán ngắt) nhưng không hiểu phần lớn những gì vị giáo sư đang trình bày một cách đầy hào hứng, và tự hỏi “độ lệch chuẩn” có nghĩa là gì, thì cũng đừng lo lắng. Khái niệm về độ lệch chuẩn trở nên vô nghĩa bên ngoài Mediocristan. Rõ ràng, sẽ hữu ích và thú vị hơn nhiều nếu bạn tham gia khóa đào tạo chuyên ngành sinh học thần kinh về mỹ học hay điệu múa châu Phi thời hậu thuộc địa, và đây sẽ là thứ dễ quan sát theo kinh nghiệm.
Các độ lệch chuẩn không tồn tại bên ngoài Gauss, hoặc nếu có, chúng cũng không có ý nghĩa và không nói lên nhiều điều. Nhưng nó sẽ trở nên tồi tệ hơn. Gia đình Gauss (bao gồm họ hàng và bạn bè, như luật Poisson) là lớp phân bổ duy nhất mà độ lệch chuẩn đó (và mức trung bình đó) có thể mô tả được. Bạn không cần gì khác nữa. Đường cong hình chuông sẽ làm hài lòng chủ trương giản hóa của những người bị đánh lừa.
Ngoài ra còn nhiều khác niệm khác có ít hoặc không có ý nghĩa bên ngoài Gauss: sự tương quan và, tệ hơn, sự hồi quy. Tuy nhiên, chúng đã ăn sâu trong các phương pháp của chúng ta; hiếm có cuộc thảo luận làm ăn nào mà người ta không nhắc đến sự tương quan.
Để thấy được mức độ vô nghĩa của sự tương quan bên ngoài Mediocristan, hãy lấy ví dụ về một chuỗi lịch sử gồm hai biến số từ Extremistan, như trái phiếu và thị trường cổ phiếu, hoặc hai mức giá chứng khoán, hoặc hai biến số khác như những thay đổi về doanh thu từ sách thiếu nhi ở Mỹ, và sản xuất phân bón ở Trung Quốc; hoặc giá bất động sản ở New York và lợi nhuận của thị trường chứng khoán Mông Cổ. Hãy đánh giá mối tương quan giữa các cặp biến số trong các giai đoạn khác nhau, ví dụ vào năm 1994, 1995, 1996, v.v. Quá trình đánh giá đó sẽ phô diễn một sự bất ổn nghiêm trọng; sự tương quan đó sẽ phụ thuộc vào giai đoạn mà nó được tính toán. Tuy nhiên, mọi người nói về sự tương quan như thể nó là thứ có thật, khiến nó trở nên hữu hình, dùng tài sản thật để đầu tư và cụ thể hóa nó.
Chính ảo tưởng về tính cụ thể đó sẽ ảnh hưởng đến cái mà chúng ta gọi là độ lệch “chuẩn”. Hãy lấy ví dụ về bất kỳ chuỗi giá hoặc giá trị lịch sử nào. Hãy chia nó ra thành nhiều phần nhỏ và đo độ lệch “chuẩn” của nó. Có gì ngạc nhiên? Mỗi ví dụ đều cho ra một độ lệch “chuẩn” khác nhau. Vậy thì tại sao mọi người lại nói về các độ lệch chuẩn? Hãy đi mà tìm hiểu.
Lưu ý rằng, giống như với lối liên tưởng ngụy biện, khi nhìn vào các dữ liệu quá khứ và ước tính một sự tương quan hoặc một độ lệch chuẩn đơn lẻ, bạn sẽ không chú ý đến tính bất ổn đó.
Nếu bạn sử dụng thuật ngữ có ý nghĩa về mặt thống kê, hãy thận trọng với những ảo tưởng về sự ổn định. Khả năng là có ai đó đã nhìn vào các lỗi quan sát của mình và cho rằng chúng thuộc Gauss, điều này đòi hỏi phải có một bối cảnh Gauss, tức là Mediocristan, để nó có thể được chấp nhận. Để chứng tỏ được mức độ đặc hữu của việc lạm dụng Gauss và mức độ nguy hiểm mà nó có thể gây ra, hãy xem xét một cuốn sách (chán ngắt) có tựa đề là Catastrophe (Thảm họa) của Judge Richard Posner, một nhà văn nổi tiếng. Posner than phiền về những hiểu biết sai lầm của “những người đày tớ nhân dân” về tính ngẫu nhiên và, bên cạnh nhiều điều khác, cho rằng các nhà hoạch định chính sách của chính phủ học môn thống kê học từ các nhà kinh tế. Có vẻ như Judge Posner đang cố kích thích để tạo ra những thảm họa. Tuy nhiên, dù là một trong những người nên dành nhiều thời gian đọc hơn viết, nhưng ông có thể là một tư tưởng gia sâu sắc và tài ba; cũng như nhiều người khác, ông không nhận thức về sự khác biệt giữa Mediocristan và Extremistan, đồng thời tin rằng thống kê học là một môn “khoa học”, chứ không thể nào là trò gian lận. Nếu bạn có tình cờ gặp anh ta, hãy bảo anh ta làm ơn chú ý đến những thứ này.
Con vật kỳ quái được gọi là đường cong hình chuông Gauss này không phải là do Gauss tạo ra. Mặc dù đã nỗ lực làm việc với nó nhưng ông chỉ là một nhà toán học đối mặt với một quan điểm lý thuyết, chứ không phải đưa ra tuyên bố về cấu trúc thực tại giống như các nhà khoa học có đầu óc thống kê. Trong cuốn “A Mathematician’s Apology” (Lời xin lỗi của một nhà toán học) G.H. Hardy đã viết như sau:
Môn toán học “thực sự” của các nhà toán học “thực sự” – như toán học của Fermat, Euler, Gauss, Abel và Riemann – hầu như đều “vô dụng” (và điều này đúng với cả toán học “ứng dụng” lẫn toán học “thuần túy”).
Như tôi đã nói trước đó, đường cong hình chuông chính là hình ảnh của một tay cờ bạc, Abraham de Moivre (1667-1754), một người Pháp tị nạn theo chủ nghĩa Canvin, đã trải qua phần lớn cuộc đời mình ở Luân Đôn dù nói bằng thứ tiếng Anh nặng trịch. Nhưng không phải Gauss mà chính Quételet – được cho là một trong những gã có tư tưởng phá hoại nhất trong lịch sử tư tưởng, như chúng ta sẽ thấy sau đây.
Adolphe Quételet (1796-1874) đưa ra ý niệm về một con người có thể chất bình thường, L’homme moyen. Chẳng có gì là moyen (bình thường) về Quételet cả, “một người có đam mê sáng tạo vĩ đại, một người tràn đầy năng lượng”, ông làm thơ và thậm chí đồng sáng tác một vở nhạc kịch. Vấn đề cơ bản với Quételet nằm ở chỗ ông là một nhà toán học chứ không phải một nhà khoa học thực nghiệm, nhưng bản thân ông lại không biết điều đó. Ông tìm thấy sự hòa hợp trong đường cong hình chuông.
Vấn đề này tồn tại ở hai mức. Thứ nhất, Quételet có một ý tưởng quy phạm (normative idea) là làm cho thế giới trùng khớp với mức trung bình của ông theo nghĩa mức trung bình đó là “bình thường”. Thật tuyệt nếu có thể bỏ qua sự xuất hiện của những thứ bất thường, “không bình thường”, Thiên Nga Đen. Nhưng hãy quay về thực tại và để giấc mơ đó cho một thế giới không tưởng.
Thứ hai, có một vấn đề rất nghiêm trọng về mặt thực nghiệm. Quételet nhìn thấy đường cong hình chuông ở khắp mọi nơi. Ông bị những đường cong hình chuông làm cho mù quáng và một lần nữa, tôi hiểu được rằng một khi trong đầu bạn đã xuất hiện một đường cong hình chuông thì sẽ rất khó lấy ra được, về sau, Frank Ysidro Edgeworth sẽ đề cập đến Quételesmus như một sai lầm nghiêm trọng của việc nhìn thấy đường cong hình chuông ở khắp mọi nơi.
Quételet tạo ra một sản phẩm hết sức cần thiết cho những khát khao tư tưởng của những người cùng thời với ông. Ông sống vào khoảng năm 1796 đến 1874, vì thế hãy xem xét danh sách những tên tuổi cùng thời với ông: Saint-Simon (1760-1825), Pierre-Joseph Proudhon (1809-1865), và Karl Marx (1818-1883), mỗi người là một phiên bản khác của chủ nghĩa xã hội. Mọi người trong thời điểm hậu Khai sáng này đều mong mỏi về thời aurea mediocritas – phương kế hành động ôn hòa: về sự giàu có, chiều cao, cân nặng, v.v. Niềm mong mỏi này bao gồm một mơ tưởng nào đó cùng với mức độ hòa hợp và chủ nghĩa Plato thật lớn. Tôi luôn nhớ lời giáo huấn của bố tôi rằng “đức hạnh nằm ở trạng thái điều tiết” (in medio stat virtus). Quả thật, điều này được xem là lý tưởng trong một thời gian dài; theo nghĩa đó, mediocrity thậm chí trở thành “khuôn vàng thước ngọc”. Một mediocrity bao hàm tất cả.
Nhưng Quételet đã nắm bắt ý tưởng đó theo một mức độ hoàn toàn khác. Thu thập các số liệu thống kê, ông bắt đầu tạo ra các tiêu chuẩn về “các phương kế”. Vòng ngực, chiều cao và cân nặng của những em bé mới sinh, tất cả đều không thoát khỏi “các chuẩn mực” của ông. Ông phát hiện ra rằng các độ lệch chuẩn trở nên hiếm hoi theo cấp số nhân khi cường độ của độ lệch đó tăng lên. Về sau, khi đã nhận biết được ý tưởng về các đặc điểm vật lý của L’homme moyen (người bình thường) này, Quételet đã chuyển sang các vấn đề xã hội. L’homme moyen có các sở thích, giả định và phương pháp của riêng mình.
Thông qua cấu trúc về l’homme moyen physique và l’homme moyen moral – người bình thường về thể chất và người bình thường về trí tuệ – Quételet đã tạo ra một phạm vi chệch khỏi mức trung bình để chia con người sang nhóm hoặc bên trái hoặc bên phải so với tâm điểm và thực sự trừng phạt những ai tự thấy mình đang chiếm giữ phần cực trái hoặc cực phải của đường cong hình chuông thống kê đó. Khi đó, chúng trở thành thứ không bình thường. Điều này đã tạo cảm hứng cho Marx, người đã trích lời Quételet về khái niệm một người bình thường hoặc một người trung bình, và đã viết trong cuốn Das Kapital như sau: “Cần phải tối thiểu hóa những độ lệch về mặt xã hội, ví dụ trong phạm vi phân bổ tài sản chẳng hạn”.
Ngày nay, con người ít nhiều phải ngợi ca sự ra đời của cơ sở khoa học thời Quételet. Nhưng thời điểm đó, những luận điểm của ông không được chấp nhận ngay. Đầu tiên, Augustin Cournot, nhà triết học/nhà toán học/nhà kinh tế học, không tin rằng một người có thể hình thành nên tiêu chuẩn của con người chỉ dựa trên các yếu tố định lượng. Một tiêu chuẩn như thế sẽ phụ thuộc vào thuộc tính đã được xem xét. Phép đo ở tỉnh này có thể khác với phép đo ở tỉnh khác. Nên lấy tỉnh nào làm chuẩn? Cournot nói rằng L’homme moyen sẽ là một con quỷ. Tôi xin giải thích quan điểm của ông như sau.
Giả sử có một điều gì đó đáng mơ ước về việc trở thành một người trung bình, anh ta phải có một đặc điểm riêng mà trong đó anh ta có tài hơn người khác – tức là anh ta không thể trung bình ở tất cả mọi điểm. Một nghệ sĩ dương cầm sẽ giỏi chơi dương cầm hơn mức trung bình, nhưng lại dở ở một điểm khác, ví dụ như cưỡi ngựa chẳng hạn. Người phác thảo sẽ giỏi về các kỹ năng phác thảo, v.v. Khái niệm về một người được cho là trung bình khác với khái niệm về một người trung bình ở những gì anh ta làm. Trên thực tế, một người trung bình chính xác phải là nửa nam nửa nữ. Quételet hoàn toàn bỏ qua điểm này.
Một khía cạnh đáng lo hơn nhiều trong phần thảo luận này chính là, vào thời của Quételet, sự phân bổ Gauss được gọi là la loi des erreurs – luật sai số, vì một trong những ứng dụng sớm nhất của nó là sự phân bố các sai số trong các tính toán về thiên văn. Bạn có lo lắng giống như tôi không? Việc lệch khỏi mức trung bình (hay còn gọi là median) đã được xem như một sai số!
Khái niệm này diễn ra rất nhanh chóng. Từ phải bị nhầm lẫn với từ là, và điều này bị hiểu là sự tán thành của khoa học. Ý niệm về người trung bình thấm sâu vào nền văn hóa với sự ra đời của tầng lớp trung lưu châu Âu, văn hóa của chủ cửa hàng tạp hóa thời hậu Napoleon, luôn thận trọng về khối tài sản quá mức và trí tuệ vượt bậc. Trên thực tế, giấc mơ về một xã hội với những kết quả bị dồn nén được cho là cách phản ứng với nguyện vọng của một người lý trí đang đối mặt với sự may rủi phát sinh. Nếu được lựa chọn một xã hội cho kiếp sau của mình nhưng không biết điều gì chờ đón, có vẻ như bạn không phải là người thích mạo hiểm; bạn thích thuộc về một xã hội với những kết quả đồng nhất (không bị chệch so với mức trung bình).
Một hiệu ứng thú vị tô điểm cho mediocrity là sự hình thành một đảng phái chính trị tại Pháp có tên là Poujadism, ban đầu gồm một chiến dịch vận động của cửa hàng tạp hóa. Đó là một sự tụ tập thân mật giữa những người gần như ủng hộ hy vọng được nhìn thấy phần còn lại của thế giới tự dồn nén thành một cấp bậc – một trường hợp về cuộc cách mạng phi vô sản. Đảng phái này có tâm lý của chủ của hàng tạp hóa, cho đến việc áp dụng các công cụ toán học. Liệu có phải Gauss đã mang toán học đến cho những người chủ cửa hàng tạp hóa chăng?
Bản thân Poincaré rất nghi ngờ về đường cong Gauss. Tôi đồ là ông đã cảm thấy buồn nôn khi được giới thiệu về nó và các phương pháp tiếp cận tương tự trong việc phác họa mô hình về tính bất định, chỉ cần hiểu rằng đường cong Gauss ban đầu được dùng để đo các sai sót về thiên văn và rằng các ý tưởng của Poincaré về việc hình thành các mô hình cơ học thiên thể đều hàm chứa ý nghĩa sâu sắc về tính bất định.
Theo Poincaré, một trong những người bạn của ông, một “nhà vật lý thực nghiệm” vô danh, đã phàn nàn rằng các nhà vật lý có xu hướng sử dụng đường cong Gauss vì cho rằng các nhà toán học tin tưởng nó như một yếu tố cần thiết trong toán học; còn các nhà toán học sử dụng nó bởi vì tin rằng các nhà vật lý nhận thấy nó là một thực tế thực nghiệm.
Ở đây, tôi xin tuyên bố rằng ngoại trừ tâm lý của cửa hàng tạp hóa kia, tôi thật sự tin vào giá trị của sự trung bình và mediocrity – có nhà nghiên cứu khoa học nhân văn nào lại không muốn giảm thiểu sự không nhất quán giữa con người? Không có gì đáng ghét hơn lý tưởng khinh suất về “siêu nhân”! Vấn đề thật sự của tôi thuộc về nhận thức luận. Thực tại là thứ không thuộc về Mediocristan, vì thế chúng ta phải học cách chung sống với nó.
Nhờ vào sự thuần khiết thuộc chủ nghĩa Plato, danh sách những người có đầu óc lúc nào cũng xoay quanh đường cong hình chuông này dài một cách đáng kinh ngạc.
Ngoài Charles Darwin ra, có lẽ Frands Galton, em họ đầu tiên của Charles Darwin và là cháu trai của Erasmus Darwin, là một trong những nhà khoa học lịch thiệp có tư tưởng độc lập cuối cùng của một danh sách gồm Lord Cavendish, Lord Kelvin, Ludwig Wittgenstein (theo cách riêng của ông), và trong chừng mực nào đó, có cả siêu triết gia của chúng ta, Bertrand Russell. Mặc dù John Maynard Keynes không thuộc lĩnh vực này nhưng lối tư duy của ông lại tiêu biểu cho nó. Galton sống vào thời Victoria, bên cạnh những sở thích như cưỡi ngựa hoặc săn bắn, thời mà những người thừa kế và nhàn rỗi, đã trở thành những tư tưởng gia, nhà khoa học hay chính trị gia (đối với những kẻ ít tài giỏi hơn). Có nhiều điều đáng khao khát vào thời đó: con người làm khoa học vì lợi ích của khoa học chứ không vì động cơ nghề nghiệp trực tiếp nào.
Thật đáng tiếc, chuyện làm khoa học vì lòng ham học hỏi và hiểu biết không nhất thiết khẳng định được rằng bạn đang đi đúng hướng. Sau khi chạm trán và tiếp thu sự phân phối “chuẩn” đó, Galton đã “chết mê chết mệt” nó. Người ta cho rằng ông đã tuyên bố là nếu người Hy Lạp biết về điều này, hẳn họ đã tôn sùng nó. Lòng nhiệt huyết của ông có lẽ đã góp phần tạo nên sự phổ biến của lý thuyết Gauss.
Galton không vinh hạnh có được hành trang toán học, nhưng lại có sự ám ảnh hiếm hoi về phép đo. Ông không biết về luật số lớn nhưng đã tái khám phá nó từ chính dữ liệu của luật này. Ông đã xây dựng nên quincunx – máy pinball hiển thị sự phát triển của đường cong hình chuông – mà chúng ta sẽ đề cập đến ở vài đoạn tiếp theo. Đúng vậy, Galton đã ứng dụng đường cong hình chuông vào những lĩnh vực như di truyền học, nơi mà tính hữu dụng của nó đã được chứng minh là đúng. Nhưng lòng nhiệt huyết của ông đã giúp thúc đẩy việc áp dụng các phương pháp thống kê mới vào các vấn đề xã hội.
Ở đây, tôi xin thảo luận về mức độ của thiệt hại đó. Nếu bạn đang đối mặt với kiểu suy luận định tính, như tâm lý học hoặc y học, việc tìm kiếm câu trả lời có/không cho các mức độ nghiêm trọng sẽ không có tác dụng, khi đó bạn có thể giả định mình thuộc về Mediocristan mà không gặp phải chút rắc rối nghiêm trọng nào. Những sự kiện được cho là không thể xảy ra có tác động không quá lớn. Bạn bị ung thư hoặc không bị ung thư, bạn mang bầu hoặc không mang bầu, v.v. Mức độ chết chóc hay mang thai không hề liên quan đến nhau (trừ khi bạn đang đối mặt với dịch bệnh). Nhưng nếu đang đối mặt với khối kết tập, nơi mà phạm vi ảnh hưởng của nó có ý nghĩa đáng kể, như thu nhập, tài sản, lợi nhuận từ các hạng mục đầu tư, hoặc doanh số bán sách, bạn sẽ gặp rắc rối và có sự phân phối không đúng nếu sử dụng đường cong Gauss vì nó không thuộc phạm vi này. Chỉ một con số đơn lẻ có thể phá vỡ toàn bộ các mức trung bình của bạn; một thất bại có thể làm tiêu tan lợi ích của cả một thế kỷ. Bạn sẽ không còn có thể nói rằng “đây là trường hợp ngoại lệ” Tuyên bố “À, tôi có thể mất tiền” sẽ không mang lại thông tin gì trừ khi bạn kèm theo đó một con số cụ thể. Có thể bạn mất hết toàn bộ số tiền có được, hoặc chỉ mất một phần thu nhập hàng ngày thôi; nhưng ở đây có một sự khác biệt.
Điều này giải thích vì sao tâm lý học thực nghiệm và những thấu hiểu của nó về bản chất con người, mà tôi đã trình bày trong những phần trước của cuốn sách này, lại có tác động mạnh mẽ đến sai lầm của việc sử dụng đường cong hình chuông; chúng cũng may mắn vì hầu hết các biến số của chúng đều cho phép ứng dụng các số liệu thống kê Gauss truyền thống. Khi tìm hiểu có bao nhiêu người trong một mẫu thử có thiên kiến, hoặc gây ra sai lầm, nhìn chung, những nghiên cứu này thường gợi ý cho kiểu câu hỏi có/không. Không có quan sát đơn lẻ nào có thể phá vỡ những phát hiện tổng thể của chúng.
Trong phần tiếp theo, tôi sẽ trình bày riêng về ý tưởng đường cong hình chuông theo hướng từ dưới lên.
Hãy xem xét chiếc máy pinball như được thể hiện trong Minh họa 8. Với 32 quả bóng, giả sử ta có một tấm ván cân bằng để quả bóng có cả hai cơ hội rơi về bên phải hoặc trái ở bất kỳ ngả rẽ nào khi ăn điểm. Kết quả mà bạn mong đợi là nhiều quả bóng sẽ chạm vào các cột ở giữa và số lượng bóng sẽ giảm khi bạn chạm vào các cột cách xa trung tâm.
Kế tiếp, hãy xem xét gedanken, một thử nghiệm tư duy. Một người sẽ tung đồng xu và sau mỗi lần tung đó, anh ta sẽ bước qua trái hoặc qua phải một bước, phụ thuộc vào mặt xuất hiện của đồng xu đó. Đây được gọi là bước đi ngẫu nhiên. Thay vì dùng bước đi, bạn cũng có thể áp dụng hình thức thắng hoặc thua l đô-la ở mỗi lần tung đồng xu, và sẽ theo dõi số tiền tích lũy mà bạn có được trong túi. Giả sử tôi bố trí bạn tham gia vào một trò đánh cược (hợp pháp), nơi khả năng thắng thua không có lợi cho bạn mà cũng chẳng có hại cho tôi. Tung đồng xu lên, nếu là mặt ngửa, bạn được 1 đô-la, nếu là mặt sấp, tôi thua 1 đô-la.
Minh họa 8: Mô hình Quincunx (đã được đơn giản hóa) – Máy Pinball

Những lần bóng rơi để ăn điểm đều có thể ngẫu nhiên rơi sang phải hoặc sang trái. Minh họa trên là kịch bản có thể xảy ra nhất là điều này rất giống với đường cong hình chuông (hay còn gọi là luật phân phối Gauss). Ảnh của Alexander Taleb.
Ở lần tung đầu tiên, bạn có hai khả năng: hoặc thắng hoặc thua.
Ở lần tung thứ hai, số lượng kết quả có thể xảy ra sẽ tăng gấp đôi. Trường hợp 1: thắng, thắng. Trường hợp 2: thắng, thua. Trường hợp 3: thua, thắng. Trường hợp 4: thua, thua. Mỗi một trường hợp đều có xác suất như nhau, sự kết hợp của một thắng và một thua đều có phạm vi ảnh hưởng gấp đôi bởi vì trường hợp 2 và 3 – thắng, thua và thua, thắng – đều có kết quả bằng nhau. Và đó là yếu tố then chốt đối với đường cong Gauss. Qúa nhiều mức ở giữa mất đi – và chúng ta sẽ thấy có nhiều mức ở giữa này. Vì thế, nếu đánh cược ở mức 1 đô-la/vòng, sau hai vòng, bạn sẽ có 25% cơ hội thắng hoặc thua 2 đô-la, nhưng có đến 50% cơ hội được hòa vốn.
Hãy tung bóng một lần nữa. Lần tung thứ ba này lại nhân đôi các trường hợp, vì thế chúng ta có tám kết quả có thể xảy ra. Trường hợp 1 (thắng, thắng trong lần tung thứ hai): thắng, thắng, thắng và thắng, thắng, thua. Chúng ta thêm một thắng hoặc thua vào cuối mỗi kết quả trước đó. Trường hợp 2: thắng, thua, thắng và thắng, thua, thua. Trường hợp 3: thua, thắng, thắng và thua, thắng, thua. Trường hợp 4: thua, thua, thắng và thua, thua, thua.
Lúc này chúng ta có tám kết quả, tất cả có thể bằng nhau. Xin lưu ý một lần nữa, bạn có thể nhóm các kết quả ở giữa, nơi mà một lần thắng sẽ bù lại cho một lần thua. (Trong mô hình quincunx của Galton, các tình huống nơi quả bóng rơi sang trái và sau đó rơi sang phải, hoặc ngược lại, chiếm ưu thế, và thế bạn sẽ có kết quả chung cuộc với nhiều mức ở giữa). Kết quả chung cuộc như sau: 1) ba thắng; 2) hai thắng, một thua, chung cuộc một thắng; 3) hai thắng, một thua, chung cuộc một thắng; 4) một thắng, hai thua, chung cuộc một thua; 5) hai thắng, một thua, chung cuộc là một thắng; 6) hai thua, một thắng, chung cuộc một thua; 7) hai thua, một thắng, chung cuộc một thua; 8) ba thua.
Trong số tám trường hợp thì trường hợp có ba lần thắng xảy ra một lần. Trường hợp ba lần thua xảy ra một lần. Trường hợp một lần thua chung cuộc (một thắng, hai thua) xảy ra ba lần.
Hãy thử thêm một lần nữa, lần thứ tư. Có thể có mười sáu kết quả tương tự. Bạn sẽ có một trường hợp với bốn lần thắng, một trường hợp với bốn lần thua, bốn trường họp có hai lần thắng, bốn trường hợp có hai lần thua, và sáu trường hợp hòa vốn.
Mô hình quincunx (từ này xuất phát từ tiếng La-tinh có nghĩa là số 5) trong ví dụ về trò chơi pinball cho thấy, lần tung thứ năm, với 64 khả năng có thể xảy ra, là lần dễ theo dõi. Đó chính là khái niệm đằng sau mô hình quincunx được Frands Galton sử dụng. Galton là người vừa không đủ lười biếng vừa hơi ngây thơ về toán học; thay và xây dựng phương pháp của riêng mình, ông hẳn đã có thể sử dụng môn đại số học đơn giản hơn, hoặc có thể thực hiện một thử nghiệm tư duy như thử nghiệm này.
Minh họa 9: Số lượng các lần thắng đã được tung
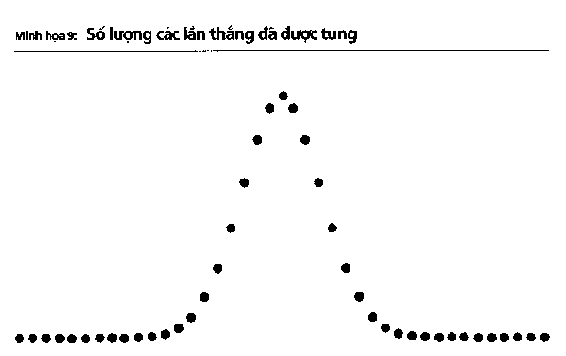
Kết quả của 40 lần tung đồng xu. Chúng ta thấy đường cong hình chuông đang xuất hiện
Hãy tiếp tục chơi cho đến khi đạt được 40 lần tung. Bạn có thể tiến hành trong vài phút, nhưng cần phải có máy tính mới có thể tính được các kết quả vì phương pháp tư duy đơn giản của chúng ta không thể nào đảm đương nổi. Bạn sẽ có khoảng 1.099.511.627.776 tổ hợp có thể xảy ra – tức hơn 1000 tỷ. Đừng phí công tính toán theo cách thủ công, quy tắc của nó là nhân đôi và cứ thế lặp lại 40 lần, vì mỗi nhánh sẽ tăng gấp đôi ở mỗi giao điểm. (Hãy nhớ lại cách chúng ta thêm một thắng và một thua vào cuối các phương pháp thay thế của lần tung thứ ba để áp dụng cho lần tung thứ tư, từ đó nhân đôi số lượng các hình thức thay thế.) Trong số những tổ hợp này, chỉ có một trường hợp trên 40 và một trường hợp dưới 40. Phần còn lại sẽ dao động ở khoảng giữa, gần 0.
Chúng ta có thể thấy rằng trong loại hình ngẫu nhiên này, các điểm cực trở nên vô cùng hiếm hoi. Trong số 40 lần tung đồng xu, chỉ có một trên 1.099.511.627.776 trường hợp là có kết quả trên 40. Nếu bạn thực hiện 40 lần tung mỗi giờ, khả năng đạt được các mức trên 40 trong một hàng sẽ thấp đến mức phải mất khoảng 40 lần tung thử mới đạt được. Giả sử dừng lại để ăn uống, nghỉ ngơi, tranh luận với bạn bè, bạn có thể phải đợi gần bốn triệu lần thời gian sống của một đời người để có cơ hội đạt được một kết quả trên 40 (hoặc một kết quả dưới 40). Và hãy xem xét trường hợp sau đây. Giả sử bạn chơi thêm một vòng nữa, để có tổng cộng là 41 lần. Để đạt được 41 lần liên tiếp toàn mặt ngửa của đồng xu, người ta sẽ mất khoảng tám triệu thời gian sống của một đời người! Khả năng này sẽ giảm xuống còn một nửa từ lần tung thứ 40 sang lần tung thứ 41. Đây là thuộc tính chính của mô hình phi thang bậc đối với việc phân tích các kết quả: các độ lệch cực độ sẽ ngày càng giảm nhanh hơn. Bạn kỳ vọng một lần trong bốn tỷ lần thời gian sống có thể tung được 50 mặt ngửa liên tiếp.
Minh họa 10: Một phiên bản trừu tượng hơn: đường cong Plato
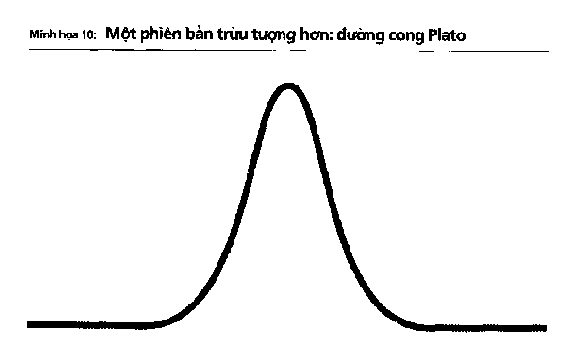
Vô số lần tung đồng xu
Dù không hoàn toàn ở trong đường cong hình chuông Gauss, nhưng chúng ta đang tiến đến gần nó một cách đáng báo động. Đây vẫn thuộc giai đoạn tiền Gauss, nhưng bạn có thể nhìn thấy thực chất vấn đề. (Trên thực tế, bạn không bao giờ có thể bắt gặp một đường cong Gauss ở dạng nguyên thủy vì nó là một dạng thức Plato – bạn chỉ đến gần chứ không thể đạt được nó). Tuy nhiên, như có thể thấy ở Minh họa 9, hình chuông quen thuộc bắt đầu xuất hiện.
Làm cách nào chúng ta có thể đến gần hơn với đường cong hình chuông Gauss hoàn hảo đó? Bằng cách hoàn thiện quy trình tung đồng xu. Chúng ta có thể hoặc tung 40 lần với mỗi lần được 1 đô-la hoặc 4000 lần với mỗi lần được 10 xu, và tổng hợp các kết quả đó lại. Rủi ro mà bạn có thể gặp phải ở hai tình huống đều như nhau – và đó là một thủ thuật. Sự tương đương trong hai đợt tung đồng xu có rất ít tình huống bất ngờ theo kiểu phản trực giác. Chúng ta nhân số lần cược đó với 100, nhưng chia quy mô cá cược cho 10 – đừng tìm hiểu nguyên nhân vào lúc này, chỉ giả định rằng chúng “tương đương”. Toàn bộ rủi ro đó đều tương đương, nhưng giờ đây, chúng ta đã có khả năng thắng hoặc thua 400 lần liên tiếp. Khả năng đó có tỷ lệ khoảng 1 trên 1 và 120 con số 0 sau đó, tức là trên 1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00 0.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00 0.000.000.000.000.000.000.000.000 lần.
Tiếp tục với quy trình này. Chúng ta di chuyển từ mức 40 lần tung với mỗi lần được 1 đô-la đến 4000 lần tung với mỗi lần được 10 xu, cho đến 400.000 lần tung với mỗi lần được 1 xu, và càng tiến gần hơn đến đường cong Gauss. Minh họa 10 cho thấy các kết quả dao động từ khoảng -40 đến 40, tức là 80 điểm plot. Lần tiếp theo sẽ nâng con số đó lên 8000 điểm.
Hãy cùng tiếp tục. Chúng ta có thể tung 4.000 lần với mỗi lần đặt cược 1/10 xu. Vậy thử tung 400.000 lần với mức cược 1/1000 xu xem sao? Như một dạng thức Plato, đường cong Gauss thuần túy chính là những gì xảy ra khi có vô số lần tung mỗi vòng, với mức đặt cược cực nhỏ. Đừng cố hình dung các kết quả đó, hay thậm chí tìm kiếm ý nghĩa của chúng. Chúng ta không thể nói về một mức đặt cược “vi phân” (vì có vô số mức đặt cược, và chúng ta đang ở trong giới hạn mà các nhà toán học gọi là cơ cấu liên tục (continuous framework). Tin vui ở đây là có một cách thay thế.
Chúng ta đã chuyển từ hình thức cá cược đơn giản sang một thứ hoàn toàn trừu tượng. Chúng ta đã di chuyển từ các quan sát đến phạm vi toán học. Trong toán học, mọi thứ đều mang một vẻ thuần túy.
Giờ đây, người ta cho rằng những thứ hoàn toàn trừu tượng không tồn tại, vì thế đừng cố gắng hiểu Minh họa 10. Chỉ cần biết được cách sử dụng nó. Hãy xem nó như một nhiệt kế: Bạn không cần phải hiểu ý nghĩa của nhiệt độ để nói chuyện với nó. Bạn chỉ cần biết được sự tương ứng giữa nhiệt độ và sự thoải mái (hoặc một lý do thực nghiệm nào đó). 600F có nghĩa là thời tiết dễ chịu, nhưng dưới 100 thì lại chẳng dễ chịu chút nào. Bạn không nhất thiết phải quan tâm đến tốc độ thực tế của những va chạm giữa các vật thể để hiểu về nhiệt độ theo cách chuyên môn. Nói cách khác, nhiệt độ là phương tiện để bạn diễn giải về các hiện tượng bên ngoài thành một con số. Tương tự, đường cong hình chuông Gauss sẽ được thiết lập để 68,2% các quan sát sẽ rơi vào giữa các độ lệch chuẩn -1 và +1 so với mức trung bình. Tôi xin lặp lại: đừng cố gắng hiểu độ lệch chuẩn có phải là độ lệch trung bình hay không – nó không phải là độ lệch trung bình, đồng thời nhiều (quá nhiều) người sử dụng từ độ lệch chuẩn này cũng không hiểu được nó. Độ lệch chuẩn chỉ là một con số mà theo đó mọi thứ được đối chiếu, một vấn đề về sự tương ứng nếu các hiện tượng thuộc đường cong Gauss.
Những độ lệch chuẩn này thường có tên hiệu là “xích-ma”. Mọi người cũng nói về “phương sai” (tương tự: phương sai là bình phương của xích- ma, tức bình phương của độ lệch chuẩn).
Hãy lưu ý tính đối xứng trong đường cong này. Bạn sẽ nhận được những kết quả giống nhau dù xích-ma đó là âm hay dương. Khả năng rơi xuống dưới mức -4 xích-ma cũng bằng khả năng vượt quá 4 xích-ma, ở đây tỷ lệ là 1 trên 32.000 lần.
Như tôi vẫn nói, bạn đọc có thể thấy được rằng điểm chính của đường cong hình chuông Gauss là hầu hết các quan sát đều xoay quanh mediocre, tức là mức trung bình, trong khi khả năng của một độ lệch chuẩn lại suy giảm ngày càng nhanh (theo cấp số nhân) khi bạn rời xa mức trung bình đó. Nếu bạn cần phải giữ lại một thông tin nào đó, hãy luôn ghi nhớ tốc độ suy giảm mạnh mẽ này khi bạn rời xa mức trung bình. Các yếu tố ngoại lai sẽ ngày càng khó xảy ra. Bạn có thể yên tâm bỏ qua chúng.
Thuộc tính này cũng tạo ra luật tối thượng của Mediocristan: căn cứ theo sự khan hiếm của các độ lệch chuẩn lớn, vai trò của chúng trong tổng thể sẽ rất nhỏ.
Trong phần ví dụ về chiều cao ở đầu chương này, tôi đã sử dụng các đơn vị lệch chuẩn 10cm, chỉ ra cách suy giảm của phạm vi ảnh hưởng khi chiều cao tăng lên. Đây là những độ lệch 1 xích-ma; minh họa về chiều cao cũng cung cấp ví dụ về hoạt động của “vẽ theo một xích-ma” bằng cách sử dụng xích-ma như một đơn vị đo lường.
Lưu ý rằng các giả định trọng tâm mà chúng ta đã đưa ra trong trò chơi tung đồng xu dẫn đến đường cong Gauss nguyên thủy, hay sự ngẫu nhiên ôn hòa.
Giả định trọng tâm thứ nhất: những lần tung đều không liên quan với nhau. Đồng xu đó không có trí nhớ. Việc bạn được mặt sấp hay mặt ngửa ở lần tung trước không ảnh hưởng đến khả năng đạt được mặt sấp hay mặt ngửa ở lần tung thứ hai. Bạn không thể trở thành người tung đồng xu “giỏi hơn” được. Nếu bạn đưa được trí nhớ hay kỹ năng vào quá trình tung đồng xu, khi đó toàn bộ đường cong Gauss sẽ không thể trụ vững được nữa.
Hãy nhớ lại các thảo luận của chúng ta ở Chương 14 về “quá trình phân phối ưu tiên” (preferential attachment) và lợi thế lũy tích (cumulative advantage). Cả hai lý thuyết này đều khẳng định rằng việc chiến thắng hôm nay sẽ khiến bạn có nhiều khả năng chiến thắng về sau. Do đó, các khả năng xảy ra sẽ phụ thuộc vào lịch sử, và giả định trọng tâm đầu tiên dẫn đến đường cong hình chuông Gauss sẽ thất bại trong thực tiễn. Dĩ nhiên, trong trò chơi, những lần thắng trong quá khứ không nhất thiết sẽ làm tăng khả năng giành chiến thắng ở những lần sau đó – nhưng điều này không diễn ra trong cuộc sống thực, đó là lý do tại sao tôi lo lắng về việc giảng dạy bộ môn xác suất từ các trò chơi. Nhưng khi việc chiến thắng dẫn đến nhiều chiến thắng hơn nữa, bạn càng có nhiều khả năng chứng kiến 40 lần thắng liên tiếp nhiều hơn so với một đường cong Gauss nguyên thủy.
Giả định trọng tâm thứ hai: không có trường hợp thay đổi “dữ dội”. Ai cũng biết rõ kích thước bậc thang của khối bêtông làm sẵn trong xây dựng là vừa cho một bước chân. Không có sự bất định trong kích cỡ của bậc thang đó. Chúng ta không gặp phải những tình huống nơi bước di chuyển đó thay đổi một cách khác thường.
Hãy nhớ rằng nếu không đáp ứng được một trong hai giả định trung tâm này, các bước di chuyển (hoặc các lần tung đồng xu) sẽ không tạo ra đường cong hình chuông. Dựa vào những gì xảy ra, chúng có thể tạo ra sự ngẫu nhiên có quy mô bất biến theo kiểu tập hợp Mandelbrot.
Một trong những vấn đề mà tôi gặp phải trong cuộc sống là bất cứ khi nào được tôi thông báo rằng đường cong hình chuông Gauss không tồn tại trong đời sống thực mà chỉ tồn tại trong suy nghĩ của các nhà thống kê học, mọi người đều yêu cầu tôi phải “chứng minh điều đó” – điều này chẳng có gì khó, như chúng ta sẽ thấy ở hai chương tiếp theo, tuy nhiên, không ai tìm cách chứng minh điều ngược lại. Bất cứ khi nào tôi đề xuất một quy trình không thuộc đường cong Gauss, người ta đều yêu cầu tôi biện minh cho đề xuất của mình và, kinh khủng hơn nữa là bảo tôi phải “cho họ thấy lý thuyết đằng sau nó”. Chúng ta đã thấy ở Chương 14 các mô hình người giàu-càng-giàu-hơn được đề xuất nhằm biện minh cho việc không sử dụng đường cong Gauss. Người ta buộc những người làm mô hình phải viết ra lý thuyết về những mô hình có thể tạo ra được tính thang bậc – như thể những người này cần phải cảm thấy hối lỗi về việc làm của mình. Lý thuyết hay “ný” thuyết! Tôi có vấn đề về nhận thức luận với điều đó, cần phải biện minh cho sự thất bại của thế giới trong việc đồng nhất là một mô hình lý tưởng mà ai đó chẳng hiểu gì về thực tiễn đã tìm cách phát triển nó.
Thay vì nghiên cứu các mô hình có thể tạo ra tính ngẫu nhiên không thuộc đường cong hình chuông để từ đó tạo ra các sai sót giống nhau trong quá trình lý thuyết hóa mù quáng, tôi đã làm điều trái ngược: tìm cách hiểu tường tận về đường cong hình chuông đến mức có thể và xác định nơi nào nó có thể tồn tại và nơi nào không. Tôi biết Mediocristan ở đâu. Đối với tôi, chính những người sử dụng đường cong hình chuông thường xuyên (hay nói đúng hơn, hầu như luôn) là người không hiểu rõ, và phải chứng minh về nó, chứ không phải những người không sử dụng. Sự xuất hiện của đường cong Gauss ở khắp nơi không phải là thuộc tính của thế giới, mà là vấn đề thuộc suy nghĩ của chúng ta, xuất phát từ cách nhìn nhận của chúng ta.
Chương tiếp theo sẽ chỉ ra quy mô bất biến của tự nhiên và các thuộc tính của tập trung phân dạng. Chương tiếp sau đó sẽ tìm hiểu về việc lạm dụng đường cong Gauss trong đời sống kinh tế xã hội và “sự cần thiết phải sản sinh ra các lý thuyết”.
Đôi khi, tôi hơi dễ xúc động vì đã trải qua phần lớn cuộc đời suy nghĩ về vấn đề này. Vì đã bắt đầu suy nghĩ về nó, và tiến hành nhiều thực nghiệm tư duy ở trên, trong cuộc đời mình, tôi chưa gặp được người nào trong giới kinh doanh và thống kê có khả năng trí tuệ nhất quán vừa tiếp nhận Thiên Nga Đen vừa chối bỏ các công cụ Gauss. Nhiều người chấp nhận ý tưởng Thiên Nga Đen của tôi nhưng lại không hiểu nó đúng với kết luận ban đầu, tức là bạn không thể sử dụng một công cụ đo lường tính ngẫu nhiên đơn lẻ được gọi là độ lệch chuẩn (và gọi nó là “rủi ro”); bạn không thể kỳ vọng một câu trả lời đơn giản sẽ nêu bật được đặc tính của sự bất định. Để tiến xa hơn nữa đòi hỏi phải có lòng can đảm, sự tận tụy, khả năng kết nối các điểm, và lòng khao khát được hiểu về tính ngẫu nhiên một cách trọn vẹn. Điều đó cũng có nghĩa là không lấy sự thông thái của người khác làm nguyên tắc chỉ đạo. Về sau, tôi bắt đầu tìm thấy các nhà vật lý – những người đã chối bỏ các công cụ Gauss nhưng lại rơi vào tội lỗi khác: sự cả tin về những mô hình dự đoán chính xác, chủ yếu là những sự trau chuốt xoay quanh quá trình phân phối ưu tiên ở Chương 14 – một dạng thức khác của Plato hóa. Tôi không thể tìm thấy người nào vừa có chiều sâu vừa có kỹ năng khoa học – người có thể nhìn vào thế giới ngẫu nhiên và hiểu được bản chất của nó, người có thể xem các tính toán như một công cụ hỗ trợ chứ không phải mục đích chính. Phải mất gần mười lăm năm tôi mới tìm thấy được nhà tư tưởng đó, người đã khiến cho nhiều thiên nga có màu xám: Mandelbrot – Benoit Mandelbrot vĩ đại.






